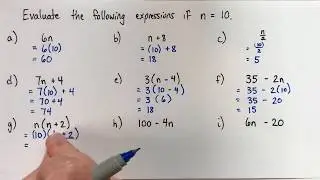How to evaluate algebraic expressions
What does it mean to evaluate an expression? How do you do it? What common mistakes should you watch out for?
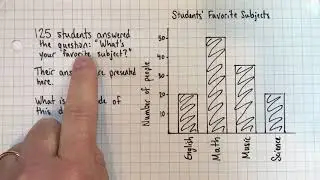
In this video, we'll be told that n=10, and we'll be asked to evaluate lots of examples of algebraic expressions that have the variable n in them.
To evaluate an expression with a variable in it, we start by substituting the value for the variable. This means that we replace the variable with the number we've been given. If we aren't given a value for the variable, we can't evaluate the expression. You should usually write the value in brackets (parentheses) when you substitute it into the expression. Sometimes it's not necessary, but sometimes it makes a big difference.
Once you're substituted the value for the variable, then all that's left is to find its value by doing whatever calculations are asked for. Remember that if there is no operation written between two numbers, by convention that means that we multiply. As you calculate, pay close attention to the order of operations. Sometimes you'll need to start with an operation in brackets, and sometimes you'll need to remember to do a multiplication or division before an addition or a subtraction, even if the addition or subtraction looks like it comes first.
In addition to teaching you how to find the answer, I'll also show you how to write your work clearly and correctly. This is especially important when there are two or more operations in the expression. Beginners often write what they're doing, but neglect to write the rest of the expression. A good answer will be a series of equivalent expression, which you can get by copying any part of the expression you haven't "done" yet to the next line.
This video is part of a playlist on representing linear relationships. Learn how to write expressions and equations, how to make tables of values, what ordered pairs are, how to find a missing value in an ordered pair, how to write precise descriptions of linear relationships, and how to create graphs. See more here: • Representing linear relationships