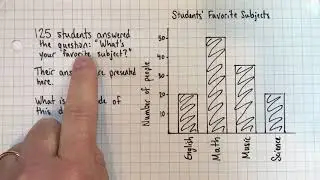
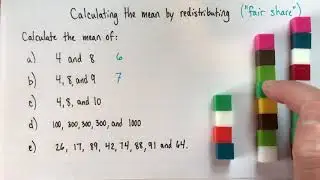Intuitive introduction to the mean with visual examples
See examples with ice cream cones to understand what the mean is, two ways of calculating it, and its main limitation.
The mean is one of several ways of finding an "average" of a group of numbers. Suppose as a first example that Alice had 2 scoops of ice cream, Betty had 1, and Charlie had 3. The mean of these numbers is the number of scoops each friend would get if they shared them equally. If Charlie gave a scoop to Betty, each friend would have 2 scoops: so 2 is the mean of 3, 1, and 2.
Another way of thinking of this sharing is to imagine collecting all of the ice cream (so we have 6 scoops altogether), and only then dividing it equally between the 3 friends. In the abstract, it's not obvious that these procedures are the same, but when you see it with the little blocks it becomes obvious. This second method, of collecting and then dividing, leads directly to the most common way of calculating the mean.
I'll show two more examples. In the second, we'll find the average of 2, 1 and 0 (since sometimes people hesitate about what to do when a set of numbers includes zero). I'll reinforce the two methods explained above.
In the third and last example, we'll imagine that Alice got 1 scoop, as did Betty. But Charlie got a little out-of-control and got 13 scoops! The reason I chose this example is to illustrate how an "outlier" (a number much bigger or much smaller than the rest) can has an outsized effect on the mean. This is one of the main drawbacks of the mean: when a small number of data points are very different from the rest, the mean may not be indicative of how "most people feel".
This video is the second in a playlist on the mean, the median and the mode. Learn what they are, how to calculate them, when each is useful, and the limitations of each. See more here: • Mean, median and mode