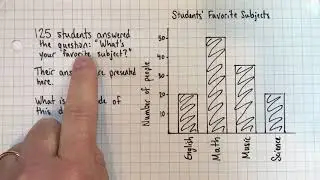
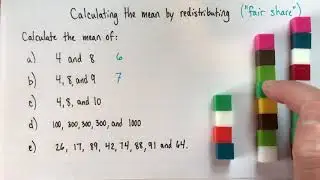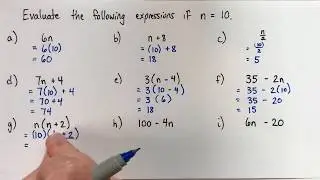What’s the difference between expressions and equations?
Expressions and equations: what's the difference? Why does it matter? Why is it important to know?
Expressions and equations can look similar, especially at first glance: they can both have variables and numbers and operations... but there's a crucial difference: the equals sign (=).
An expression is a meaningful combination of mathematical symbols, including numbers, variables, operations, and brackets/parentheses. An equation, on the other hand, is a statement that two expressions are THE SAME, or equal.
Expressions and equations are both useful mathematical objects! They're great shorthands that can contain lots of information. But one of the most important differences to understand is the difference in what we can DO with them: we can EVALUATE expressions, and we can SOLVE equations.
Sometimes we will want to EVALUATE an expression. That means that we find its value. If the expression has one or more variables in it, we will need to be given the value of the variables to do so. If you don't know what x represents, you can't evaluate x–3! But if, for example, you know that x=10, then you can say that x–3 = 10–3 = 7.
Sometimes we will want to SOLVE an equation. This means finding the value(s) of the variable(s) that make the equation true (in other words, that give both sides of the equation the same value). For example, we can solve the equation 14x+15=71... we get x=4. That means that if x is 4, then 14x+15 has a value of 71. To be clear, you can't solve an expression.
This video is part of a playlist on representing linear relationships. Learn how to write expressions and equations, how to make tables of values, what ordered pairs are, how to find a missing value in an ordered pair, how to write precise descriptions of linear relationships, and how to create graphs. See more here: • Representing linear relationships