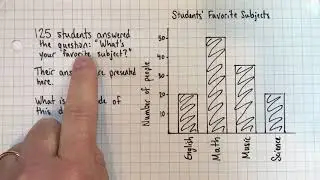
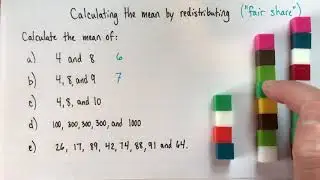Calculate the mean by finding the sum and dividing
Learn how to calculate the mean for any set of numbers, learn WHY it gives you an average, and learn how to organize your work.
One method of calculating the mean is to add up all of your numbers (i.e. find the sum), and then divide by the number of numbers you have. But why does that give you an average?
I'll use some of the examples I talked about in my video on finding the mean by sharing: • Calculate the mean by sharing In that video, we represented our numbers with cubes, and redistributed them until every pile was the same size (equal sharing, or fair sharing).
In this video, instead of just redistributing the cubes to share them equally, I'll make a tiny change to the procedure: first, we'll collect them all, THEN we'll divide them equally.
So if we're finding the mean of 4, 8 and 9, first we collect everything into a pile. How many cubes are in that pile? Well, 4+8+9, or 21 cubes. Then we'll pass them back out into the three piles, the same number as we had at the start. So how much will each pile get? Well, 21/3=7, so seven. The mean of 4, 8 and 9 is 7.
This method, while slightly slower with cubes, is significantly easier when we're dealing with large sets, or "messy" numbers. And it's very easy to formalize into two steps, or even a formula. First, add up all of your numbers; then divide that sum by the number of numbers in your original set!
I'll show three examples to make sure you understand.
This video is part of a playlist on the mean, the median and the mode. Learn what they are, how to calculate them, when each is useful, and the limitations of each. See more here: • Mean, median and mode