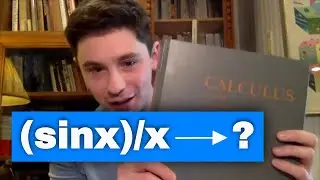Skepticism about Mathematical Beauty (Jeff Breeding-Allison) | Ep. 13
Jeff Breeding-Allison is a number theorist and data scientist. We discuss the concept of mathematical beauty: what the phrase is meant to convey, what might make a piece of mathematics beautiful, and whether it is useful to pursue an ideal like beauty in mathematics.
0:00 Intro
1:09 The general issue of mathematical beauty
5:43 What does it matter if math is beautiful or not? Beauty in art vs. beauty in math.
8:19 What drives mathematicians to choose to do math? Truth, beauty, and utility.
10:49 Justifying research in mathematics. Michael Harris' Mathematics without Apologies. Beauty as pleasure for the person doing the mathematics.
13:49 How is the pleasure of doing mathematics different from the pleasure of other problem-solving activities? Possible answer: math produces eternal truths, which satisfy us.
17:28 Appreciation of math that was done by someone else. Euler's identity.
23:18 Two proofs of the sum 1 + 2 + 3 + ... + n = n(n+1)/2. Is one more beautiful?
30:05 How something is true vs. why something is true. Different proofs that there are infinitely many prime numbers.
36:33 Cleverness. Do we prefer proofs that hide the thought process?
38:39 The problems given in Russian university entrance exams to discriminate against Jewish applicants.
42:11 Proofs that reveal distinctions and give rise to new definitions. How the way math is written obscures the process of discovery. The way normal subgroups were introduced.
49:55 Examples of ugly mathematics/unimportant mathematics.
55:35 G.H. Hardy's aesthetic criteria of unexpectedness, inevitability, and economy. How important is unexpectedness, and how can one prove something unexpected? Proof as confirming intuition vs. being the main issue.
1:01:23 The classification of compact continuous symmetry groups and the discovery of exceptional Lie groups.
1:03:40 Why the math that I do is ugly and why I don't mind.
1:13:35 Math that is bad by virtue of offering partial results but no possibility of answering the real question at hand. Odd perfect numbers.
1:17:38 Major disagreement over whether beauty inheres in finding the perfect framework a la Grothendieck.
1:23:26 My preference for the "genetic" approach to mathematics. Works of H.M. Edwards.
1:26:25 How different proofs look like when starting from different perspectives. What I've learned from doing my series on Tricky Parts of Calculus. What we ask from a proof depends on context.
1:32:26 What about utility as a virtue for math? Some mathematicians take pride in the uselessness of their work.
1:35:37 Rebuttal: many mathematicians not concerned with applications during the work process. Discussion of applications as guide to math in history. Is there an application for quadratic reciprocity?
1:41:18 What is abstract and what is concrete?
1:45:45 Sabine Hossenfelder's criticism of theoretical physicists' obsession with beauty and naturalness. Could beauty lead math astray? What is the goal of mathematics?
1:55:34 Atiyah's fMRI study on mathematical beauty.
1:59:57 Ed Frenkel's The Rites of Love and Math. The Langlands philosophy.
2:05:26 Conclusions
Check out my channel for more great conversations and math content: / @danielrubin1
Daniel Rubin Show full episodes playlist: • Daniel Rubin Show, Full episodes
My previous conversation with Jeff about modularity of elliptic curves and math careers outside academia: • Modularity of Elliptic Curves | Math ...
My Tricky Parts of Calculus playlist: • Tricky Parts of Calculus
This is a series of lectures on subtle parts of calculus that are rarely covered in a calculus class.
Please like, comment, subscribe, and hit the notification bell!
Books mentioned:
E.H. Gombrich, The Story of Art https://amzn.to/3es3OqI
Michael Harris, Mathematics without Apologies: Portrait of a Problematic Vocation https://amzn.to/3rjqJK1
G.H. Hardy, A Mathematician's Apology https://amzn.to/3B8D0Wt
Aigner and Ziegler, Proofs from the Book https://amzn.to/3evxOC7
H.M. Edwards, Galois Theory https://amzn.to/3in1KBv
H.M. Edwards, Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory https://amzn.to/3ew2ALf
H.M. Edwards, Riemann's Zeta Function https://amzn.to/3zcj5DZ
Ed Frenkel, Love and Math: The Heart of Hidden Reality https://amzn.to/36FLnuH
Sabine Hossenfelder, Lost in Math: How Beauty Leads Physics Astray https://amzn.to/3zaqJPg
(I get a small commission from purchases made from these links.)
ArXiv version of my paper with Alex Townsend and Heather Wilber on Faber rational functions: https://arxiv.org/abs/1911.11882
Benedict Gross, On the Langlands correspondence for symplectic motives http://people.math.harvard.edu/~gross...
Zeki, Romaya, Benincasa, Atiyah, The experience of mathematical beauty and its neural correlates https://www.maths.ed.ac.uk/~v1ranick/...


![[A M V] Между нами километры](https://images.mixrolikus.cc/video/hvmyrLjnlRQ)