Perfect Numbers and Elementary Methods in Modern Research (Josh Zelinsky) | Ep. 15
Josh Zelinsky is a number theorist and teacher at the Hopkins school in New Haven, CT. We discuss his experience as a former academic teaching high school mathematics and his research to address whether there are any odd perfect numbers, one of the oldest unsolved problems in mathematics. Key issues: what makes for a good research problem? and are elementary techniques underutilized?
Timestamps
0:00 Josh's career
1:55 Advanced mathematics and research at a private high school
7:25 Teaching at a private high school vs. college/university
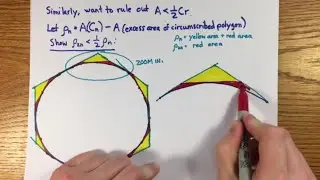
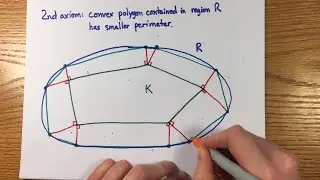
21:30 The problem of perfect numbers
29:44 Why study odd perfect numbers
34:23 Justifying funding for math research
37:31 What techniques can you use to study perfect numbers? Consequences for the rest of math
40:23 What are sieve methods?
45:03 Some history of modular arithmetic
54:11 More fundamental mathematical techniques: complex analysis, theory of modular forms
58:53 When the first natural object of investigation is the tough case
1:03:18 Picking a research problem with consideration to career. What if you don't think you can solve the problem?
1:12:52 The state of number theory today. The drive to use modern techniques when elementary techniques suffice.
1:21:07 More trends in number theory. Dustin Clausen and Peter Scholze's "condensed mathematics" project.
1:27:41 Too much abstraction in number theory? The Weil conjectures
1:33:29 Mochizuki's purported proof of the abc conjecture
1:39:02 A proof strategy for avoiding errors
1:43:43 What math should people learn in school?
1:50:53 Critical thinking: it's importance and how it's proponents usually just want people to think like they do
1:55:00 Math to prepare people for jobs. The scarcity of good jobs in academia
2:05:41 The influence of PROMYS on the way we teach
Dustin Clausen's interview on Math-Life Balance: • Interview with Dustin Clausen
PROMYS webpage: https://promys.org/
Books mentioned:
H.M. Edwards, Riemann's Zeta Function https://amzn.to/2VndqMQ
H.M. Edwards, Fermat's Last Theorem: A Genetic Approach to Algebraic Number Theory https://amzn.to/3B0Z1qf
H.M. Edwards, Galois Theory https://amzn.to/3AQFVCX
H. Iwaniec and E. Kowalski, Analytic Number Theory https://amzn.to/3AXvi13
William H. Brock, The Chemical Tree: A History of Chemistry https://amzn.to/3i3z54y
Paul Pollack, Not Always Buried Deep https://amzn.to/3k7DfLs
Julia Galef, The Scout Mindset: Why Some People See Things Clearly and Others Don't https://amzn.to/2T2leCT
(I get a small commission from purchases made from these links.)
![[FREE] Big Yavo Type Beat](https://images.mixrolikus.cc/video/ipZpeZuo4bE)
