Math Dispute Breakdown: In Defense of Analysis

Опубликовано: 18 Август 2021
на канале: Daniel Rubin

7,935

249

Summary of my discussion with Professor NJ Wildberger on whether we can admit the notions of infinity that appear in the theory of analysis. I try to make my arguments more clear, add some comments about what we discussed, and set up the important points for further debate.

My discussion with Norman Wildberger: • Math Debate: Real numbers and the inf...

More episodes of my podcast, featuring fascinating discussions of math and other topics: • Daniel Rubin Show, Full episodes

0:00 What the dispute is about
2:35 My 3 objections to Norman's view
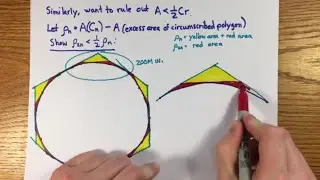
3:54 Norman's example: whether there is a solution to x^3 = 15. Where we disagree
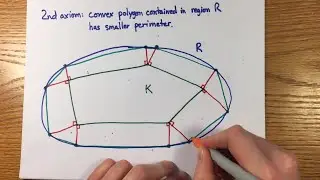
8:58 The Axiom of Infinity
10:45 What do we require of a mathematical theory for it to be comprehensible?
12:19 Analysis is a successful theory, so why attack it?
14:25 My view of Norman's example of the geocentric model of the universe
16:35 Why I think it's not useful to insist on correct foundations at the outset
17:23 Addressing Norman's points about the development of math
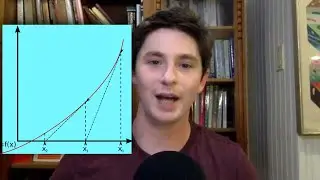
20:40 Examples of the success of the modern analytical theory of functions and power series
23:43 Why I don't consider Norman's issue with pi + e + sqrt(2) to be a crisis for the theory of real numbers
27:17 Questions about a finitist framework

I make reference here to the view in the philosophy of science put forward by Thomas S. Kuhn. His famous work in which he spells out this view is The Structure of Scientific Revolutions https://amzn.to/3CXlZPN

Interestingly, Norman brought up the dispute over the geocentric and heliocentric models of the universe, which is the subject of another of Kuhn's books, The Copernican Revolution https://amzn.to/2VWQvZG

Both of these are fantastic books that I highly recommend. The Copernican Revolution explains really well some of the earliest science of astronomy and its historical development. The Structure of Scientific Revolutions is a must-read for anyone remotely interested in the philosophy of science or its history.