5 Methods to Introduce the Exponential Function and Logarithm WITH PROOFS
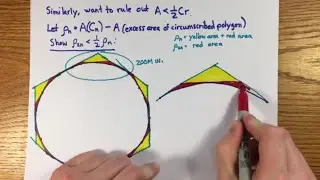
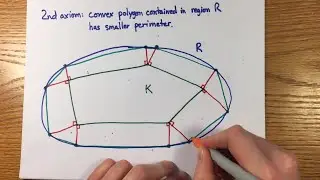
Here are multiple methods to introduce the exponential and logarithm functions and derive their properties from first principles. I give several proofs that are rarely done in a calculus class, including: extending exponentiation to irrational numbers, convergence of (1+1/n)^n, derivative of an exponential function, recovery of other properties when exp is defined as the solution of a differential equation, power series solution to y'=y, recovery of limit definition of e^x when log(x) is defined as an integral.
This is Episode 5 of my series on the Tricky Parts of Calculus.
0:00 Intro
1:56 Method 1: Extending exponentiation to all real numbers
7:31 Method 2: The additive-multiplicative property, or functional equation f(x+y) = f(x)f(y)
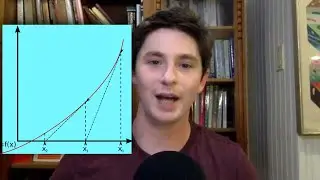
9:00 Derivatives of exponentials, the number e as the limit (1+1/n)^n
19:33 Method 3: The differential equation y' = y with y(0) = 1
21:28 Method 4: Constructing a power series solution to the differential equation
23:35 Method 5: Defining the logarithm as the integral of 1/t from 1 to x
Article on discontinuous functions satisfying f(x+y) = f(x)f(y): http://math.mit.edu/~stevenj/exponent...
Check out the other videos in my Tricky Parts of Calculus series for complete proofs and discussions of subtle issues usually glossed over in a calculus class.
Tricky Parts of Calculus playlist: • Tricky Parts of Calculus
Also check out my channel for general advice and opinions about math, as well as the Daniel Rubin Show podcast for interesting conversations about math and other topics: / @danielrubin1