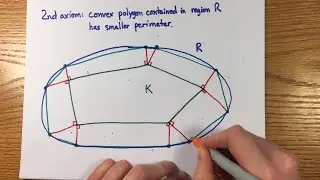
Modularity of Elliptic Curves | Math PhDs Outside Academia (Jeff Breeding-Allison) | Ep. 11

Опубликовано: 11 Январь 2021
на канале: Daniel Rubin

1,513

Jeff Breeding-Allison is a number theorist and a professional data scientist. We discuss Jeff's work in number theory, and I ask him about they key steps in the proof that elliptic curves are modular (the result that proved Fermat's Last Theorem). Then we discuss Jeff's transition out of academia, career prospects for mathematicians, and the consequences of the bleak career landscape for academic mathematics.

Helpful links:
https://en.wikipedia.org/wiki/Wiles%2...
https://en.wikipedia.org/wiki/Siegel_...
https://en.wikipedia.org/wiki/Ellipti...
https://www.ams.org/notices/200706/tx...

0:00 Number theory, my first love in math
5:20 Math background (p-adics, Langlands program, representation theory, modular forms, algebraic geometry, L-functions)
14:54 The Plimpton 322 tablet and Pythagorean triples
23:00 Fermat's Last Theorem and Wiles' proof of modularity. Where is the hard work?
27:17 What does it mean that a curve is modular? Functional equations for L-functions. Hasse-Weil theorem.
30:28 Some technical points about FLT. Galois representations.
39:00 Modular forms. Hecke operators. Construction of a curve with same data as a modular form.
50:13 From elliptic curves to modular forms.
57:25 The roles of algebra and analysis in math. Stepanov's polynomial method.
1:06:11 Learning algebraic number theory. HM Edwards' excellent book Fermat's Last Theorem: A Genetic Approach to Algebraic Number Theory.
1:11:16 Jeff's work on the Paramodular Conjecture and modularity for higher dimensional abelian varieties.
1:32:01 Jeff's transition from academic math to data science.
1:41:16 The difficulty of training in math or science for a job in the real world.
1:57:21 How math education might change to address the need for jobs.
2:08:44 Differences between doing math and doing data science/machine learning.
2:13:53 Online vs. in-person learning. My plans to give some online lessons.