Sin(x), x, tan(x) inequalities and Archimedes' axiom of convexity | Tricky Parts of Calculus, Ep. 2

Опубликовано: 14 Март 2021
на канале: Daniel Rubin

2,897

122

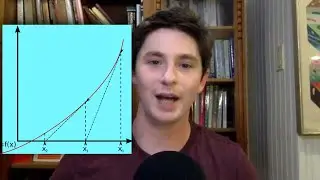
I prove the key inequalities involving sin(x), x, and tan(x) that are necessary to compute the derivative of the sine function.

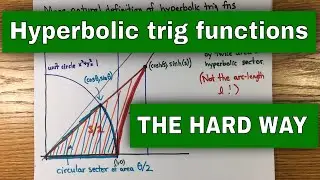
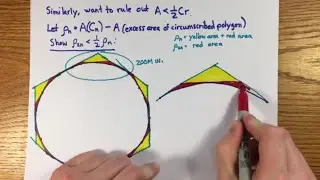
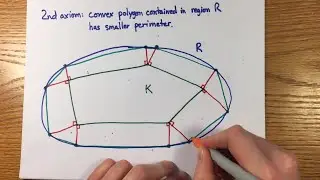
I show how Archimedes dealt with these inequalities in the context of comparing the circumference of a circle to the perimeters of inscribed and circumscribed polygons, with emphasis on the special role of convex curves. Then I give modern commentary on Archimedes' axioms. This lays the groundwork for determining the area constant of a circle and estimating pi.

This is Ep. 2 in a series of videos on the subtle and difficult parts of calculus that are usually not emphasized in a calculus class.

Ep. 1: • Derivative of sin(x), CAREFUL PROOF |...

#pi

#calculus