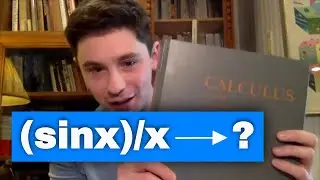Modular forms, G2, and Bloch-Kato (Sam Mundy) | Ep. 18
Sam Mundy is a number theorist and NSF postdoc at Princeton University. We discuss his new paper "Eisenstein series for G2 and the symmetric cube Bloch-Kato conjecture". The Bloch-Kato conjecture is a generalization of the Birch and Swinnerton-Dyer conjecture relating the order of vanishing of the L-function of an elliptic curve at its central point to the rank of its group of global solutions, a Clay Math Millennium Problem. Sam explains the conjecture's key players: modular forms and Galois representations, and the significance of the exceptional compact simple Lie group G2 in his work.
0:00 Intro
3:02 Sam's educational background
12:55 Number theory yields "real results"
16:28 Getting into research. Sam's major weight loss.
26:23 Explaining number theory to a general audience. Prime factorization, Gaussian integers.
35:56 The Langlands correspondence
41:00 The big ideas of Sam's paper.
46:45 Galois representations attached to modular forms
55:13 How Bloch-Kato generalizes BSD
1:01:12 References for this subject
1:04:56 Back to Bloch-Kato. Selmer groups. Sam's result.
1:27:32 Automorphic forms and G2
1:47:07 Outline of the proof and techniques used. p-adic deformation theory.
2:08:45 What's next? Why attack a more general problem when BSD is still unproven?
2:16:04 Lattice cryptography and a modular forms approach to solving lattice problems
Sam's webpage: https://web.math.princeton.edu/~sm7928/
Sam's paper Eisenstein series for G2 and the symmetric cube Bloch-Kato conjecture https://arxiv.org/abs/2202.03585?fbcl...
Links to books mentioned:
Diamond and Shurman, A First Course in Modular Forms https://amzn.to/3IqSus9
McKean and Moll, Elliptic Curves: Function Theory, Geometry, Arithmetic https://amzn.to/3K0kVgG
Roy, Elliptic and Modular Functions from Gauss to Dedekind to Hecke https://amzn.to/3M8iuuA
(I get a small commission from purchases made from these links.)


![[A M V] Между нами километры](https://images.mixrolikus.cc/video/hvmyrLjnlRQ)