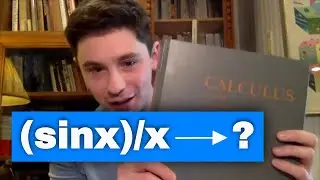YOU CAN'T USE EULER'S IDENTITY TO PROVE THE ANGLE SUM IDENTITIES! | Tricky Parts of Calculus, Ep. 4

Опубликовано: 02 Апрель 2021
на канале: Daniel Rubin

3,347

108

I give multiple proofs of the angle sum identities sin(x+y) = sin(x)cos(y) + sin(y)cos(x) and cos(x+y) = cos(x)cos(y) - sin(x)sin(y) from different perspectives. I stress that a very common presentation of these formulas based on Euler's identity e^(ix) = cos(x) + i sin(x) is circular and should not be considered a legitimate proof.

Outline:
Intro
How angle sum identities follow from Euler's identity
How to prove Euler's identity
Different approaches to Euler's identity (is it possible to prove without the angle sum identities?)
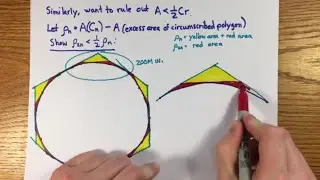
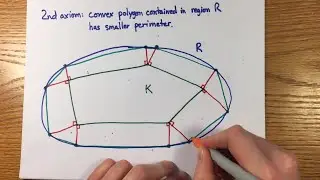
Elementary proof of angle sum identities using Law of Cosines
Original proof (Law of the Broken Chord)
Proof by representation of rotations by matrices
Differential equations proof
History of the angle sum identities

Check out the other videos in my Tricky Parts of Calculus series for complete proofs and discussions of subtle issues usually glossed over in a calculus class.
Tricky Parts of Calculus playlist: • Tricky Parts of Calculus

Also check out my channel for general advice and opinions about math, as well as the Daniel Rubin Show podcast for interesting conversations about math and other topics.

Here's a reference for showing how the Law of the Broken Chord gives the angle difference formula for sin: https://www.mathpages.com/home/kmath2...