public key crypto intro 2
A motivating example of a public-key communication.
(Not a secure example, but just one which tries to show that it's plausible that a secret can be communicated in the presence of eavesdroppers, with no pre-arrangement.)
Typo at 4m22s: "Could you have told me that the secret number was *858*?"
(not "286" as stated in video).
Contents:
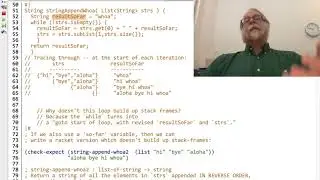
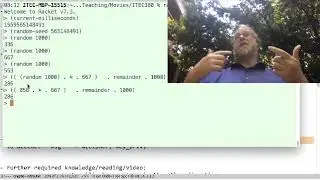
0m55s: Give a particular encryption system `e` to use as our example.
1m41s: create a secret-message that I don't even know (but that we can verify later).
2m50s: encrypt the secret-message (the 4th number from a random-number-generator)
3m43s: de-crypt the original message in my head (and verify that it encrypts to the secret version)
4m42s: explain that I multiplied by the private-key (3) to un-do the multiplication by public-key (667)
[After this, you might now believe at a gut level, that a public-key system is conceivable.]
5m53s: Mention that the scheme shown here can be broken by mathematicians.
6m47s: So, why did the particular numbers 3 and 667 work together?
7m25s: verify that the 4th random-number in the sequence above really was 858.
8m05s: what does "digitally sign"?
Further small clarifications, perhaps not fully stated in the video:
1m41s: Since we have no volunteer, I'll create for a secret-number that I don't even know -- to do this, I'll use the fourth number from a "random number generator", but first we'll initialize ("seed") that generator using the time-of-day-in-milliseconds, a number I can't predict.
7m20s: "Okay, I see 3*667 = 2001, and 2001 ≡ 1 (mod 1000). But how did you come up with those two such numbers?" Well, if I can find two numbers that multiply to negative one (-1), then I can negate either of them and they'll multiply to +1. And -1≡+999 (mod 1000), and so really I just need to find two numbers that multiply to 999. One such choice is 3 and 333 (and there are other factorings I could have used too). So I negated one of them (-333≡+667 (mod 1000)), so +667 and +3 work as a public,private key that complement each other. I could also have used 333 and -3≡+997 as the public & private keys. ... but I have a harder time multiplying by either of those numbers in my head :-)
You can equally-well use other factors of -999 (like ⟨+111,-9⟩, or ⟨+27,-37⟩). And if you want to use something different than 1000 (a different "modulus"), you certainly can use 1,000,000 or 43 or 2987349234 instead -- so long as you can figure out divisors of that-number-minus-1.
But as mentioned in video: Euclid's extended algorithm will let people crack this code.
Hint: real-world RSA is based on a similar idea, except instead of multiplying two numbers (and taking remainder) to get 1, you raise one to the other (and take remainder, using a modulus that is prime) to get 1. While mathematicians know how to undo multiplication-in-presence-of-remainder, they don't know how to undo exponentiation-in-presence-of-remainder (the "discrete logarithm" problem) -- or at least not how to do so feasibly for large numbers. Perhaps someday somebody will figure it out, and RSA will become a broken crypto-system?