Meanfield models for populations of quadratic integrate-and-fire neurons for non-Cauchy distribution

Опубликовано: 05 Январь 2021
на канале: Denis Goldobin

141

Talk by Denis S. Goldobin
Seminar on Complex Oscillatory Systems

Title:
Low dimensional macroscopic dynamics of populations of quadratic integrate-and-fire neurons beyond the Lorentzian ansatz

Abstract:
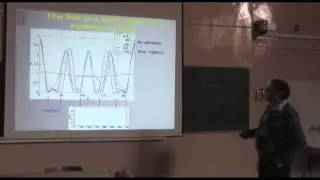
The populations of quadratic integrate-and-fire neurons are known to form a Lorentzian distribution (LD) of states of individual elements for several important network models [PRX 5, 021028 (2015)]. These states are equivalent to the Ott-Antonsen ansatz in terms of phase variables. For an evolving LD, one can derive a low-dimensional equation system governing the dynamics of the mean membrane voltage and the firing rate. In some practically important setups, e.g. with endogeneous and external noise (external noise is not with a common signal), the LD of distribution is distorted and the original low-dimensional model becomes inapplicable. We present an approach based on the characteristic function representation of the probability density deviating from the LD. For such a function ordinary cumulants (and moments) diverge, but one can introduce alternative objects, ‘pseudo-cumulants’. The real and imaginary parts of the first pseudo-cumulant are the firing rate and the mean voltage; higher pseudo-cumulants introduce small corrections to their dynamics.
Joint work with Matteo di Volo and Alessandro Torcini.
D.S.G. Funding: RSF-DFG grant no. 19-42-04120

pdf: https://drive.google.com/file/d/1-5gT...
PowerPoint presentation: https://drive.google.com/file/d/1GjJ4...