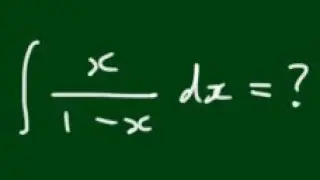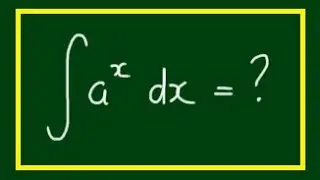The Multiplicative Inverse of a Complex Number

Опубликовано: 17 Декабрь 2014
на канале: MasterWuMathematics

20,090

312

The multiplicative inverse of a complex number exists such that z∙z^-1 = 1. To find the inverse, let z = a+ib and z^-1 = c+id.

Now, when we multiply z and z^-1, we get:

z∙z^-1 = (a+ib)(c+id)=ac+iad+ibc+i^2bd=(ac-bd)+i(ad+bc)

Knowing the result that z∙z^-1 = 1, we can equate the components:

ac-bd = 1
ad+bc = 0

Solving these simultaneously, we can get c and d in terms of a and b, such that

c = a/(a^2+b^2)
d = -b/(a^2+b^2)

Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

Chat with me on Twitter! / masterwumath