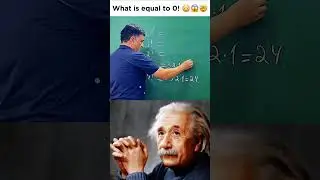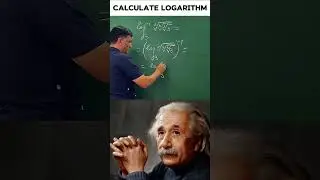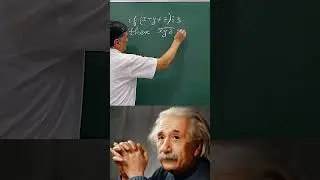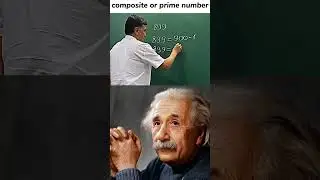Yangi to'plam. 65-dars. Darajali funksiyalar. Kasr-ratsional funksiyalar. Matematika.
Darajali funksiyalar. Kasr-ratsional funksiyalar
Darajali funksiya - u=x° koʻrinishdagi funksiya.
D arajali funksiya jukovskiy funksiyasi Reja: 1. D arajali funksiya 2. Jukovskiy funksiyasi. D arajali funksiya Ushbu nz W ko’rinishdagi funksiya darajali funksiya deyiladi, bunda n – natural son. Bu funksiya butun kompleks tekislikda golomorf. 0 1 n nz W shart 0 z nuqtalarda bajariladi. Demak nz W funksiya }0{\ C sohadagi har bir z nuqtada konform ekan. Z=0 nuqtada konformlikning buzilishini shu nuqtada burchak kattaliklarining saqlamasligi ham ko’rsatadi
Elementar funksiyalarni darajali qatorga yoyishga doir masalalar o’rganib chiqildi. Bunda avvalo nazariy qismi berildi. So’ngra misollar va ularni yechilishlari berligan. Ishning maqsad va vazifalari. Nazariy bilimlarni amaliyotga tadbiqi va undan foydalanishni ko’rsatish. Ob’yekti va predmeti. Mavzuni Elementar funksiyalarni darajali qatorga yoyish va eyler formulalari, ba’zi elementar funksiyalarni darajali qatorga yoyish hisoblash tashkil etadi. Predmenti o’quv adabiyotlari, darsliklardagi ma’lumotlarni tashkil etadi
Xususan bazis funksiyalar sifatida darajali funksiyalar lar olinsa bog’lanish. ko'rinishda izlanadi. Bu yerda noma’lum koeffitsiyentlarni shunday aniqlash kerakki, tuzilgan (8.1) n – darajali ko’phad jadval qiymatlarga to’la mos kelsin.Bu shartlarga ko’ra larni aniqlash uchun quyidagi n+1 noma’lumli n+1 ta chiziqli algebraik tenglamalar sistemasini hosil qilamiz. Bu sistemani yechib, aniqlangan qiymatlarini (8.1)ga qo’yilganda hosil bo’lgan ko’phad interpolyatsion ko’phad deyiladi. interpolyatsion ko’phadga qo’yiladigan yagona va
Ratsional funksiyalarni integrallash. Oldingi paragrafda har qanday elementar funksiya integrali yana elementar funksiyadan iborat bo‘lishi shart emas ekanligini misollarda ko‘rsatgan edik. ... Demak, har doim noto‘g‘ri ratsional kasrni ko‘phad (butun funksiya) va to‘g‘ri ratsional kasr yig‘indisi kabi ifodalash mumkin. Masalan, noto‘g‘ri ratsional kasr suratini maxrajiga ustun usulida bo‘lib, uni. ko‘rinishga keltira olamiz
Kasr-ratsional funksiyalarni integrallash. Quyidagi. (11.1). ko‘rinishdagi kasrga. kasr-ratsional funksiya. yoki qisqacha. ratsional funksiya. deyiladi
Ratsional funksiyalar — oʻzgaruvchi x va ixtiyoriy sonlar ustida bajarilgan arifmetik amallar (qoʻshish, ayirish, koʻpaytirish va boʻlish) natijasida oxirgi son hosil boʻladigan funksiya. Ratsional funksiyalarning integrali Ratsional funksiyalarlar yigʻindisi, logarifmik va arktangens funksiyalar orqali hisoblanadi. Ratsional funksiyalar va ixtiyoriy sonlar ustida bajariladigan arifmetik amallar natijasida olingan oxirgi son, Ratsional funksiyalarning hosilasi ham Ratsional funksiyalar boʻladi
Ratsional kasrlarni integrallash. Ikkita ko’phadning nisbati ratsional kasr deyiladi. Pn (x) Qm (x). . Bunda n m bo’lsa. ratsional kasr to’g’ri ratsional kasr deyiladi, n³m bo’lsa, ratsional kasr noto’g’ri. ratsional kasr deyiladi. Bunday kasr suratini maxrajiga bo’lish bilan butun va kasr. ... ya’ni Qm (x) =1 bo’lsa, kasr butun ratsional funksiyaga aylanadi. Buni integrallash. yuqorida ko’rib o’tilgan. Endi to’g’ri ratsional kasrni integrallashni ko’rib o’tamiz. Avval oddiy ratsional. kasrlarni integrallashni ko’ramiz
Funksiya — matematikaning eng muhim va umumiy tushunchalaridan biri. Funksiyaning turlari koʻp boʻlib, eng koʻp qoʻllaniladigani bu chiziqli funksiyadir yaʼni. . Oʻzgaruvchi miqdorlar orasidagi bogʻlanishni ifodalaydi va muhim.
00:00 ► Yangi to'plam. Matematika yangi taxrirdagi to'plam
00:32 ► 1. Agar y=x²-4x+7 va 0 katta yoki teng x kichik yoki teng 5 bo’lsa, funksiya qanday oraliqda o’zgaradi?
03:23 ► 2. y=(x-1)(x²+3x-5) funksiya grafigi OY o’qni qaysi nuqtada kesib o’tadi?
04:07 ► 3. y=(x+1)(x²-7x+5) funksiya OX o’qni nechta nuqtada kesib o’tadi?
05:19 ► 4. f(x)=x³-7x-6 va g(x)=x³+6x²+11x+6 funksiyalar grafiklari nechta umumiy nuqtaga ega?
06:16 ► 5. Parallel ko’chirish natijasida ustma-ust tushadigan funksiyalar qaysi?
08:04 ► 6. y= (x+1)/(x+2) funksiya grafigi qaysi chorakda yotadi?
10:00 ► 7. y= (x-2)/(x+3) funksiya qiymatlar sohasini ko’rsating
11:10 ► 8. I-usul. y= (x+3)/(x-2) funksiyaning kamayish oralig’ini ko’rsating.
12:12 ► 8. II-usul. y= (x+3)/(x-2) funksiyaning kamayish oralig’ini ko’rsating.
13:37 ► 9. y=(x²+9)/x funksiya eng kichik qiymatini toping
14:11 ► 10. I-usul. y=(x²-4x+6)/(x²-4x+5) funksiya qiymatlar to’plamini toping.
15:33 ► 10. II-usul. y=(x²-4x+6)/(x²-4x+5) funksiya qiymatlar to’plamini toping.
#Funksiya #daraja #kasr #darajali_funksiya #kasr_funksiya