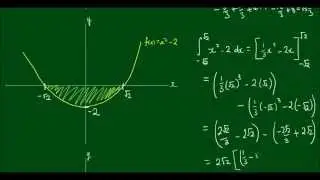
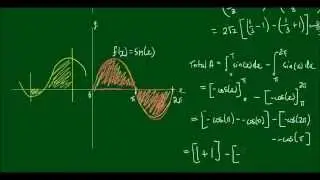
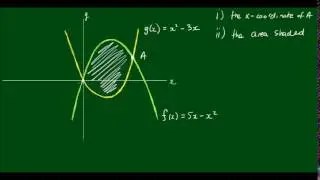
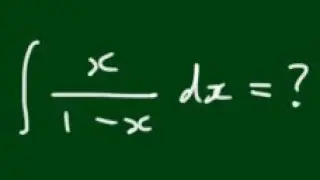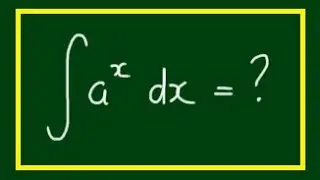Proof: Limit as x approaches 0 of [tan(x) - x] / x^3 = 1/3 (L'Hospital's Rule)

Опубликовано: 09 Март 2021
на канале: MasterWuMathematics

2,277

In this video, we use L'Hospital's Rule to prove that the limit as x approaches 0 of [tan(x) - x] / x^3 is equal 1/3.

Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world. Please donate here: https://paypal.me/MasterWu

Follow me on Twitter! twitter.com/MasterWuMath