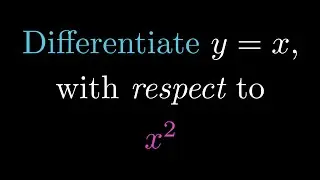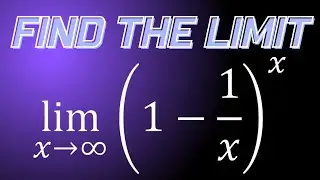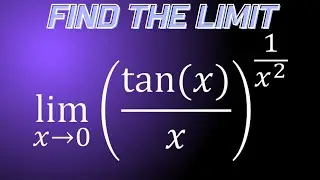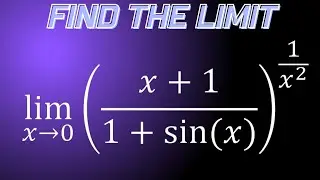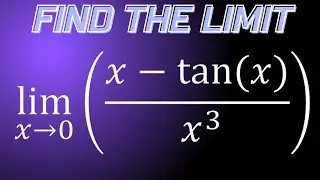Limit of (x-2)^3+8/x as x approaches 0
In this video we find the limit of (x-2)^3+8/x as x approaches 0. Each step is explained carefully. We expand the cubic term in the numerator using the Perfect Cube Formula. This allows us to factor out an x term in the numerator and cancel it with the x term in the denominator. At this point we are no longer dividing by 0, so we can just let x=0 in the limit, arriving at our final answer of 12.
If you found this content useful make sure to SUBSCRIBE and check out some of my other videos! If you have any questions about this video or other mathematics please feel free to leave them in the comment section below. If you have an alternative solution, please leave it in the comment section below! Thanks for watching.
I have linked some videos below which I think you may find useful! If you are struggling on this topic make sure to check them out!
Limit of x^2-16/x^2+3x-4 as x approaches -4:
• Limit of x^2-16/x^2+3x-4 as x approac...
Limit of 1+cos^3x/sin^2x as x approaches pi:
• Limit of 1+cos^3x/sin^2x as x approac...
Limit of 1+cosx/sinx as x approaches pi:
• Limit of 1+cosx/sinx as x approaches pi
Limit of (1+a(e^-x-1))^-1/x as x approaches 0:
• Limit of (1+a(e^-x-1))^-1/x as x appr...
I hope you have a great day!