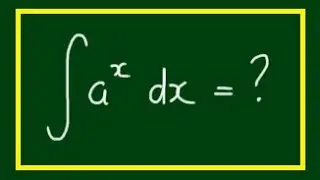The Product Rule of Differentiation - Example x^2 tan(x)
In this video, we find the differential of the function x^2*tanx by considering it as a product of 2 functions, x^2 and tanx. This allows us to apply a method called the Product Rule, which helps us to find the derivative with relative ease.
The product rule is defined as:
d/dx(u*v) = v*du/dx + u*dv/dx
Or in shorthand form:
(u*v)' = vu' + uv'
So if we let...
u = x^2
v = tan(x)
The derivatives of u and v are...
du/dx = u' = 2x
dv/dx = v' = sec^2(x)
We can then substitute these terms according into the product rule to find the derivative of x^2*tan(x)
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
To see the derivative of tanx, please review this video - • Derivative of tan(x)