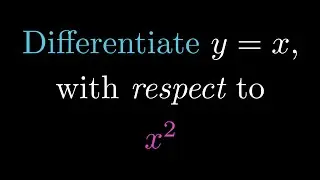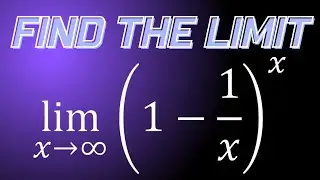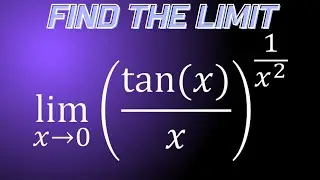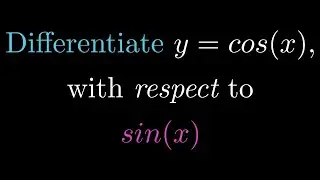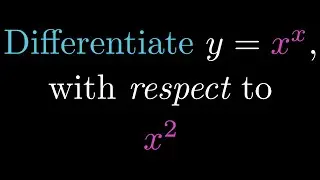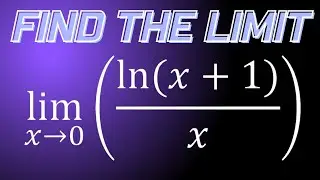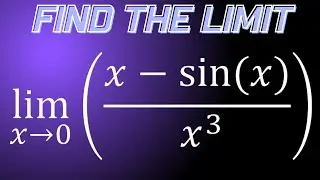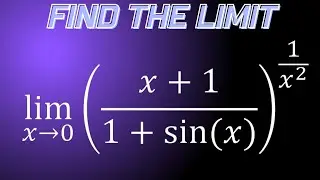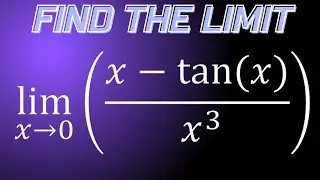Limit of e^x-1/x as x approaches 0
In this video we find the limit of x^x as x approaches zero from the right.
Each step is explained carefully . We make use of the properties of the natural logarithm and exponential function. We also utilise L'Hopital's rule when required. Limit Laws are taken for granted in this problem.
If you found this content useful, make sure to SUBSCRIBE and check out some of my other videos! Thanks for watching I hope you have a great day. All questions are welcome.
I have linked some videos below which I think you may find useful! If you are struggling on this topic make sure to check them out!
Limit of x^x^x as x goes to 0+ :
• Limit of x^x^x as x goes to 0+
Limit of (1+x)^(1/x) as x approaches 0 :
• Limit of (1+x)^(1/x) as x approaches 0
Limit of (x/x+a)^x as x approaches infinity:
• Limit of (x/x+a)^x as x approaches in...
Derivative of lnx by first principles (no L'Hopital's rule):
• Derivative of lnx by first principles...
I hope you have a great day!