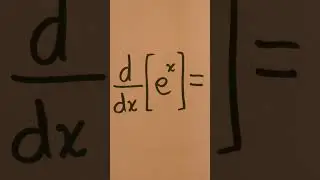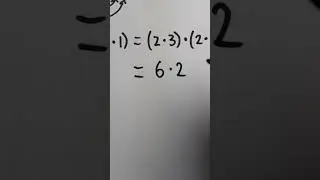Limit of sin(kx)/x as x approaches 0 | Calculus 1 Exercises

Опубликовано: 12 Октябрь 2022
на канале: Wrath of Math

5,928

108

We show the limit of sin(kx)/x as x goes to 0 is equal to k, even when k=0. To evaluate this trigonometric limit, we need to remember the limit of sin(x)/x with x approaching 0, which is a fundamental trigonometric limit equal to 1! If we remember this, we'll be able to solve the problem in short order by multiplying by k/k. #Calculus1 #apcalculus

Limit of sin(2x)/x as x approaches 0:    • Limit of sin(2x)/x as x approaches 0 | Cal...
Proof for Limit of sin(x)/x: (coming soon):

Calculus 1 Exercises playlist:    • Calculus 1 Exercises
Calculus 1 playlist:    • Calculus 1

◉Textbooks I Like◉
Graph Theory: https://amzn.to/3JHQtZj
Real Analysis: https://amzn.to/3CMdgjI
Proofs and Set Theory: https://amzn.to/367VBXP (available for free online)
Statistics: https://amzn.to/3tsaEER
Abstract Algebra: https://amzn.to/3IjoZaO
Discrete Math: https://amzn.to/3qfhoUn
Number Theory: https://amzn.to/3JqpOQd

★DONATE★
◆ Support Wrath of Math on Patreon for early access to new videos and other exclusive benefits:   / wrathofmathlessons
◆ Donate on PayPal: https://www.paypal.me/wrathofmath

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Thanks to Crayon Angel, my favorite musician in the world, who upon my request gave me permission to use his music in my math lessons: https://crayonangel.bandcamp.com/

Follow Wrath of Math on...
● Instagram:   / wrathofmathedu
● Facebook:   / wrathofmath
● Twitter:   / wrathofmathedu

My Math Rap channel:    / @mathbars2020